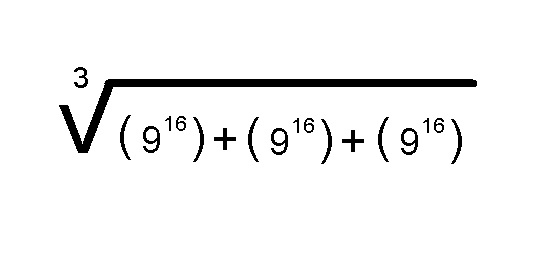-
Guía de Matemáticas con las Pol Power Calculator
Encuentra en esta guía matematica de las calculadoras Pol Power Calculator
las definiciones e informaciones más relevantes e inovadoras sobre el tema matemático
para mejorar tus resultados en matemáticas generales para informática y computación.

Matemáticas 1: Matemáticas Generales Para Informática
Estos Son los 20 Artículos de Matemáticas 1: Matemáticas Generales Para Informática
2025/10/18 12:37:47 , Sábado
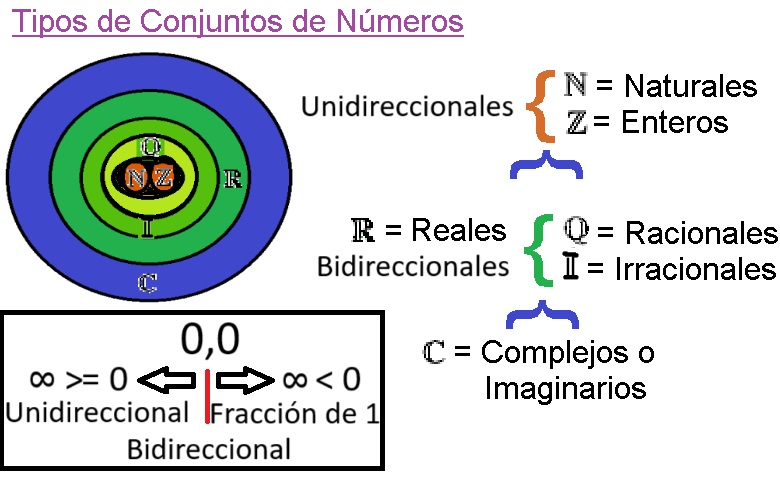
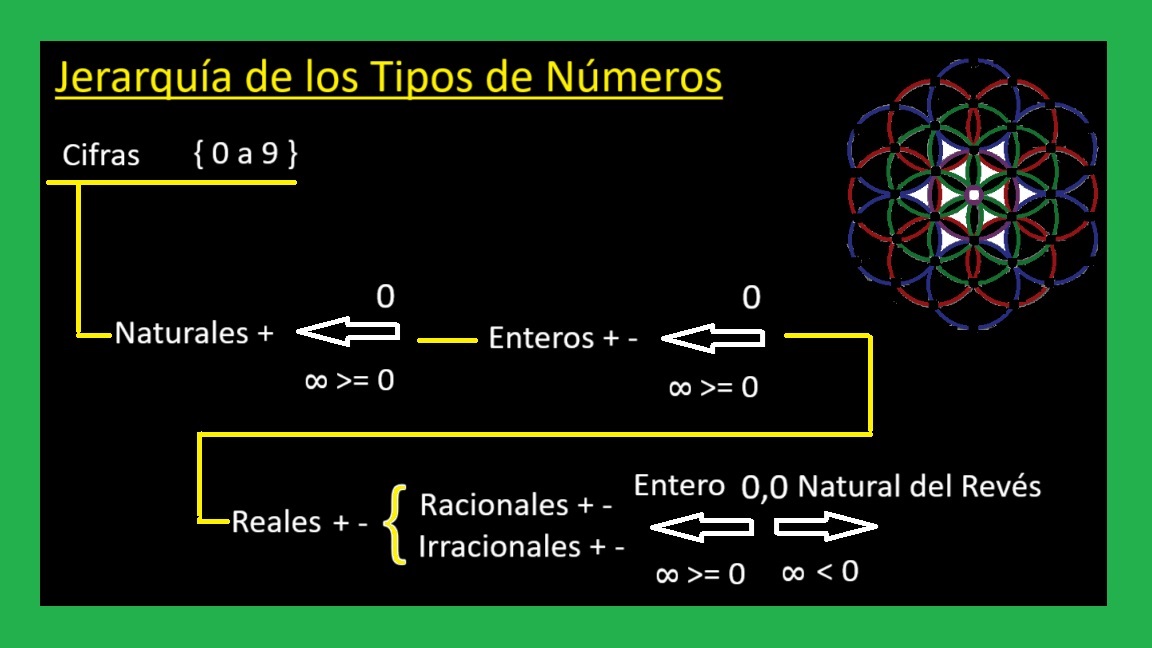
01 ¿Que Tipos de Numeros y Simbolos Existen?
01 Definicion de Numero y Tipos de Numeros Que Existen

2025/10/17 13:42:13 , Viernes
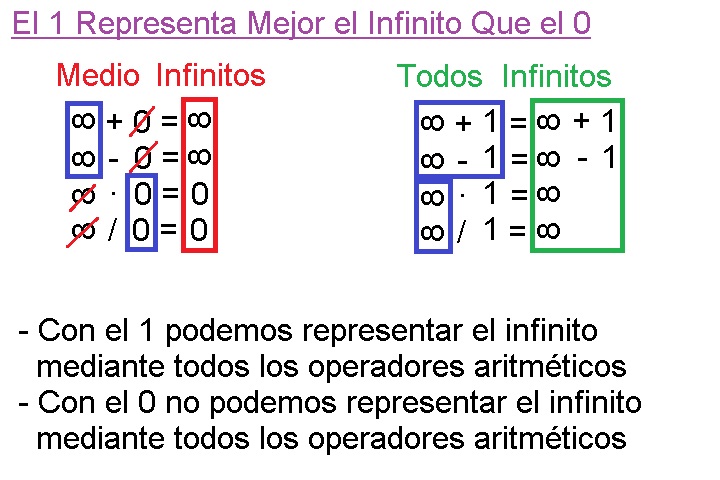
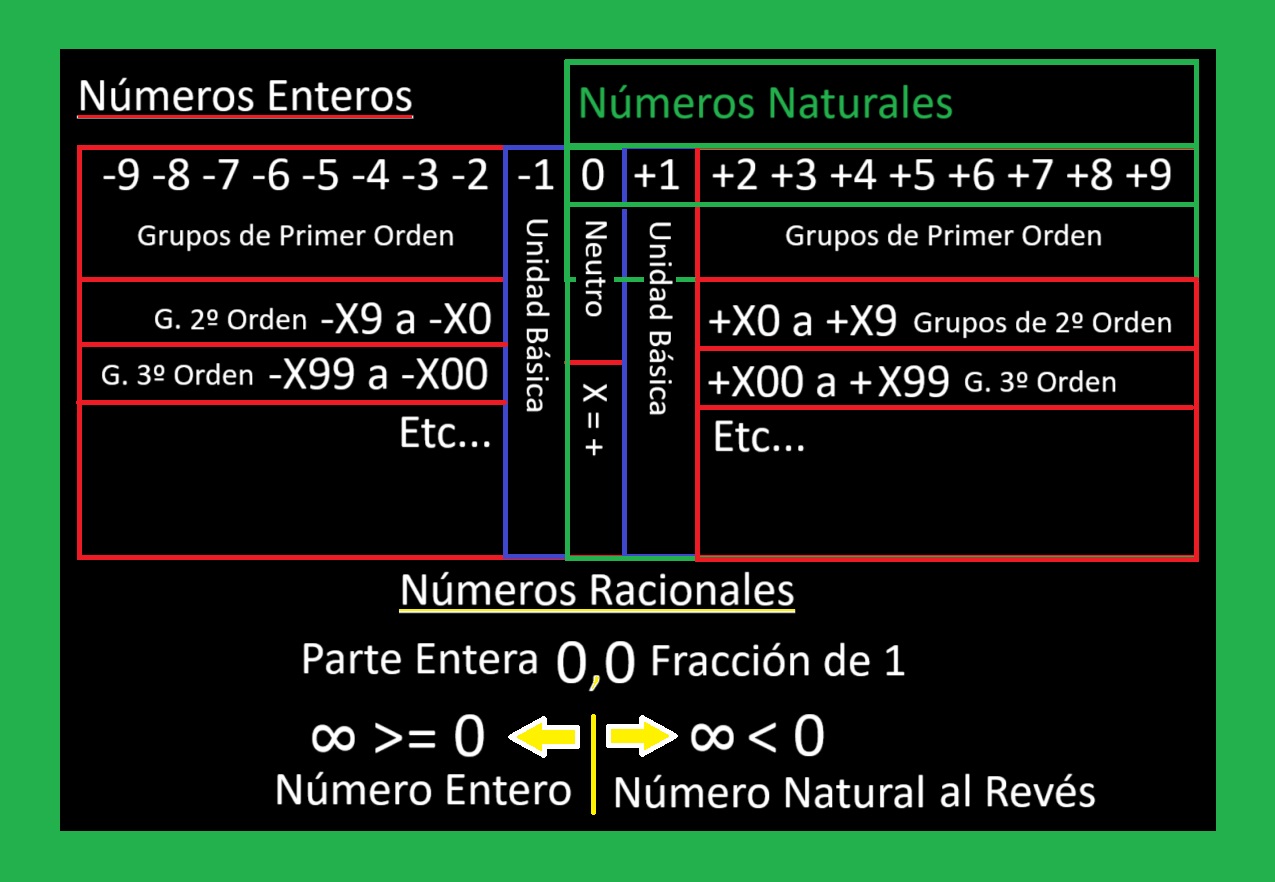
Cuatro Puntos Clave el 0 el 1 el 2 y el 3
El 0 es un Numero Neutro Que Separa Lo Positivo de lo Negativo

2025/10/12 15:55:16 , Domingo
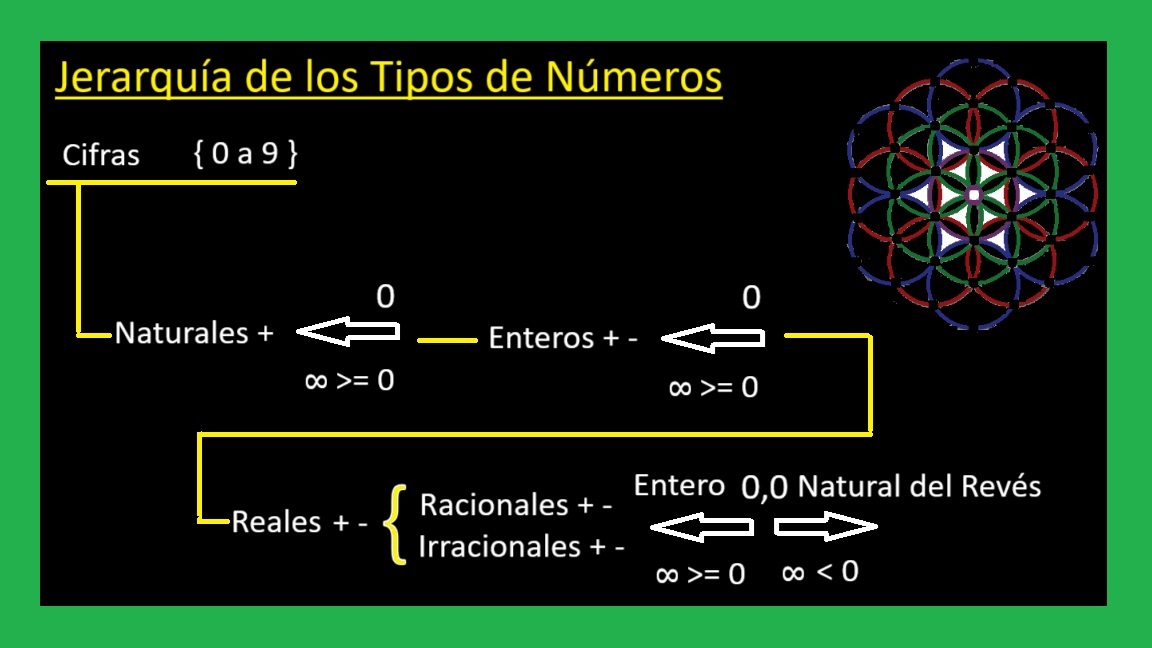
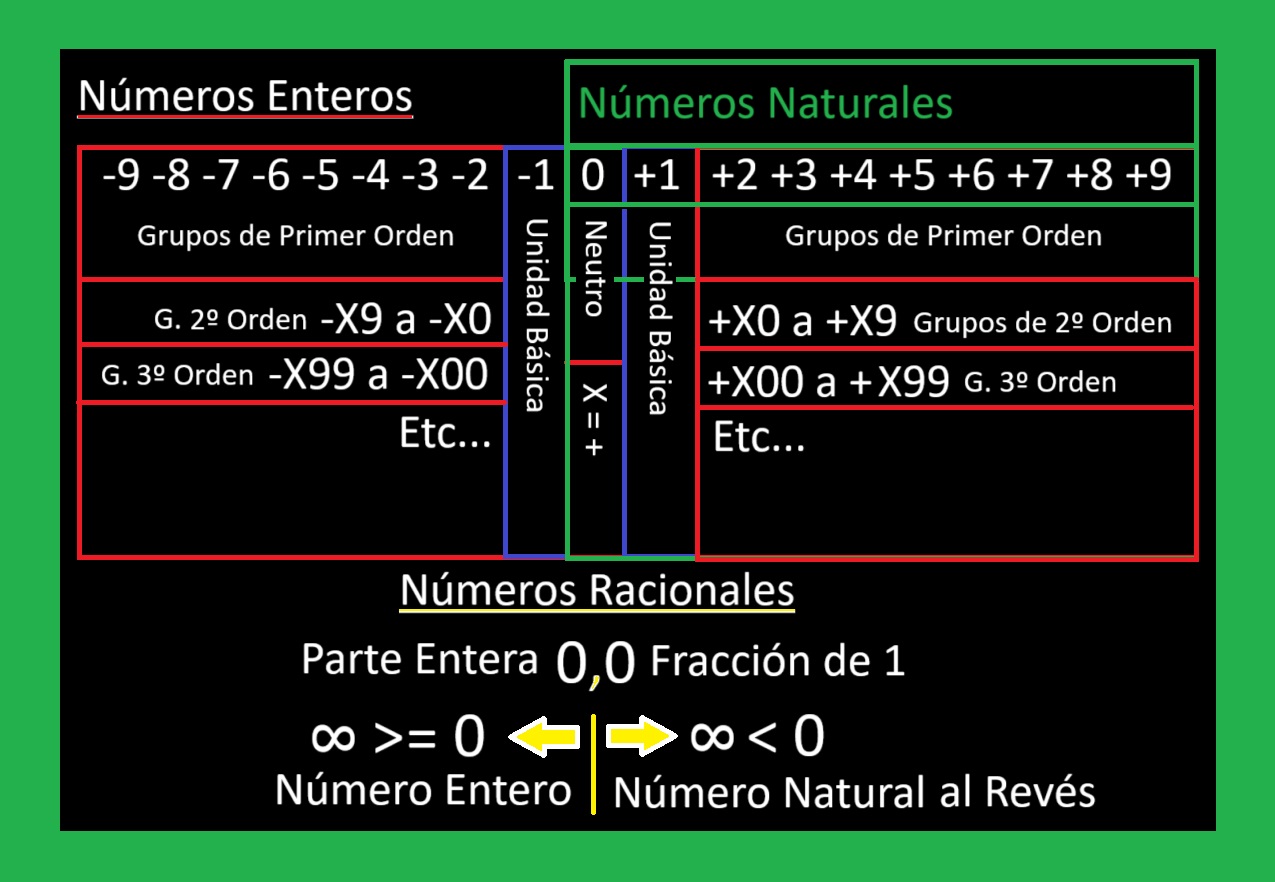
La Importancia de los Numeros Naturales
01 Numeros Basados en Naturales Por Norma

2025/01/20 14:35:24 , Lunes
La Logica del Byte
01 Definicion de BIT y BYTE Segun Pol


2025/03/31 16:22:44 , Lunes
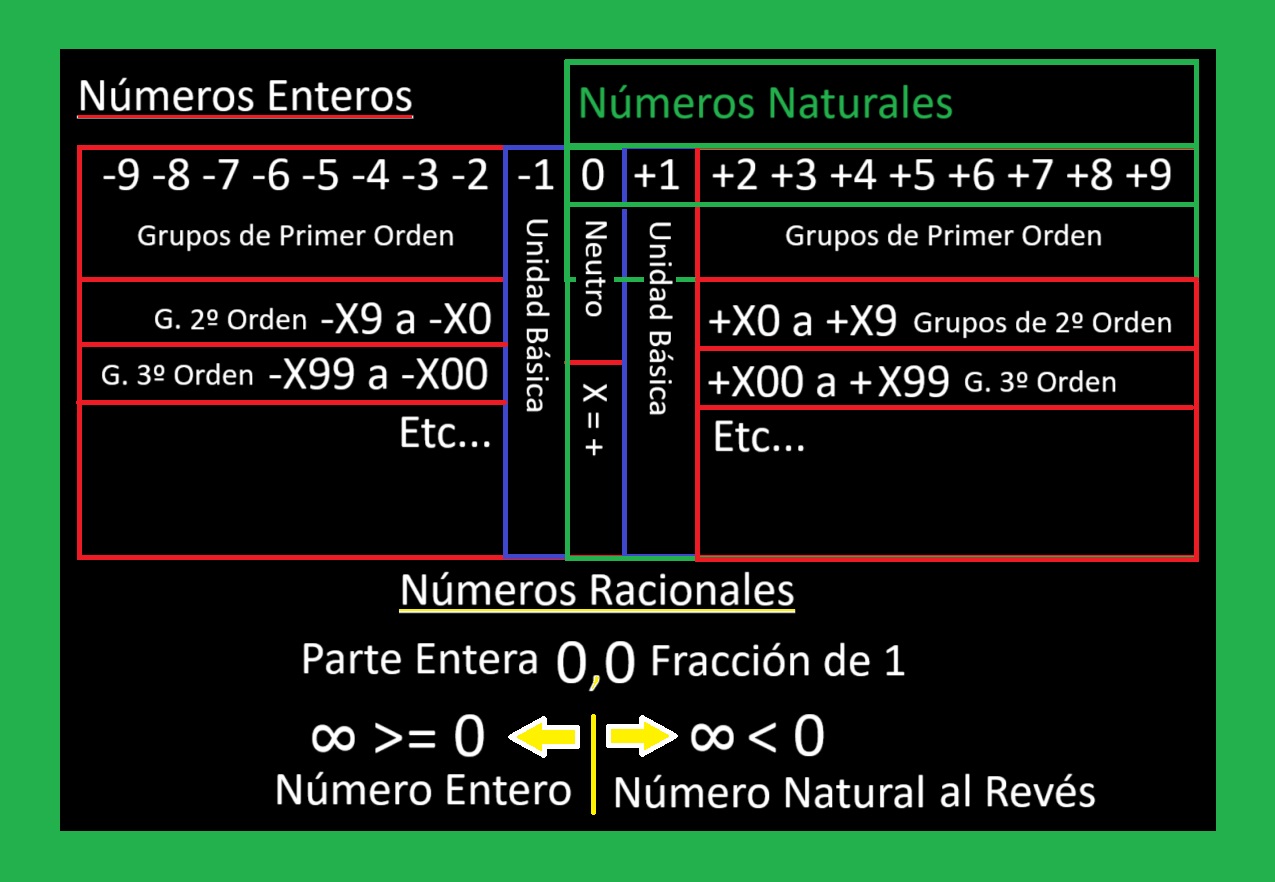
01 ¿Que son las Bases Numericas?
01 Definicion de Base Numerica Segun Pol

2023/05/08 15:48:45 , Lunes
02 ¿Que es el Algebra y la Aritmetica?
Que es el Algebra

2023/05/08 22:40:02 , Lunes
03 ¿Que son las Ecuaciones?
01 Que son las Ecuaciones

2025/02/11 14:17:24 , Martes
04 Jerarquia de Funciones Segun Su Existencia
Jerarquia de Funciones de Operador Segun Su Existencia


2023/05/31 16:17:40 , Miércoles
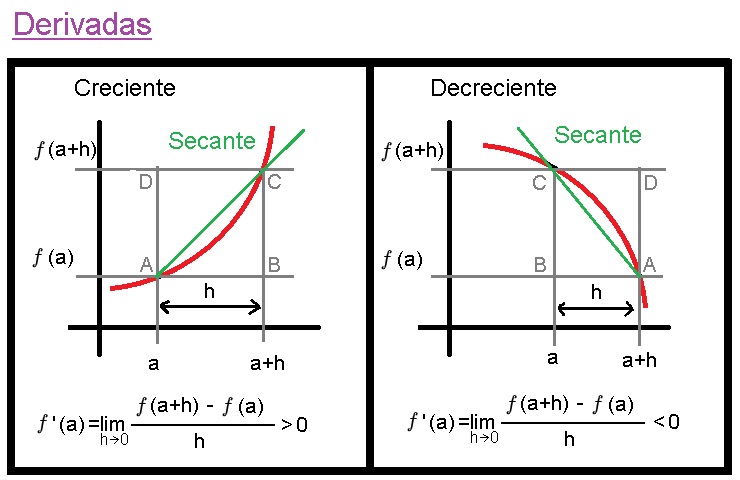
05 ¿Que es una Derivada?
Que son las Derivadas
2024/05/16 21:19:28 , Jueves
06 ¿Que es un Limite?
Definicion de Numero Limite en Matematicas
2025/09/16 15:18:57 , Martes
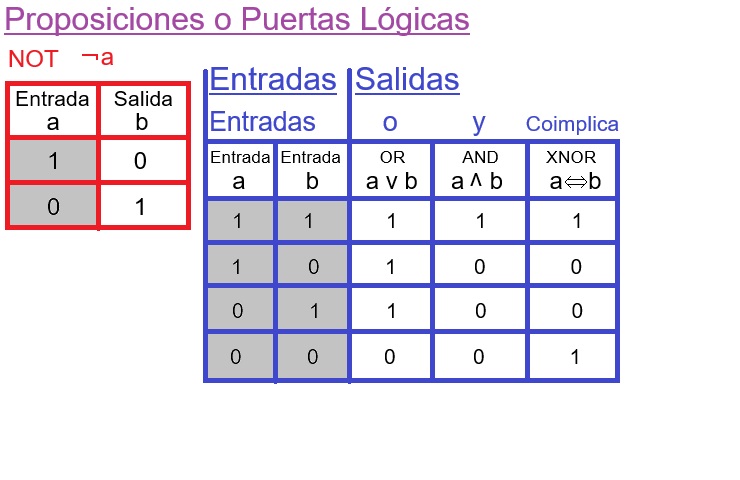
¿Que son las Puertas Logicas o Compuertas Logicas?
Algebra de Boole; Puertas Logicas o Compuertas Logicas
2025/09/16 14:51:48 , Martes
Series y Sumatorias
01 Definicion de Serie Secuencia o Sucesion Segun Pol



2025/02/20 17:44:45 , Jueves
¿El Infinito es Real o Natural?
El Infinito es Natural Aunque Sea Real

2025/09/01 14:31:49 , Lunes
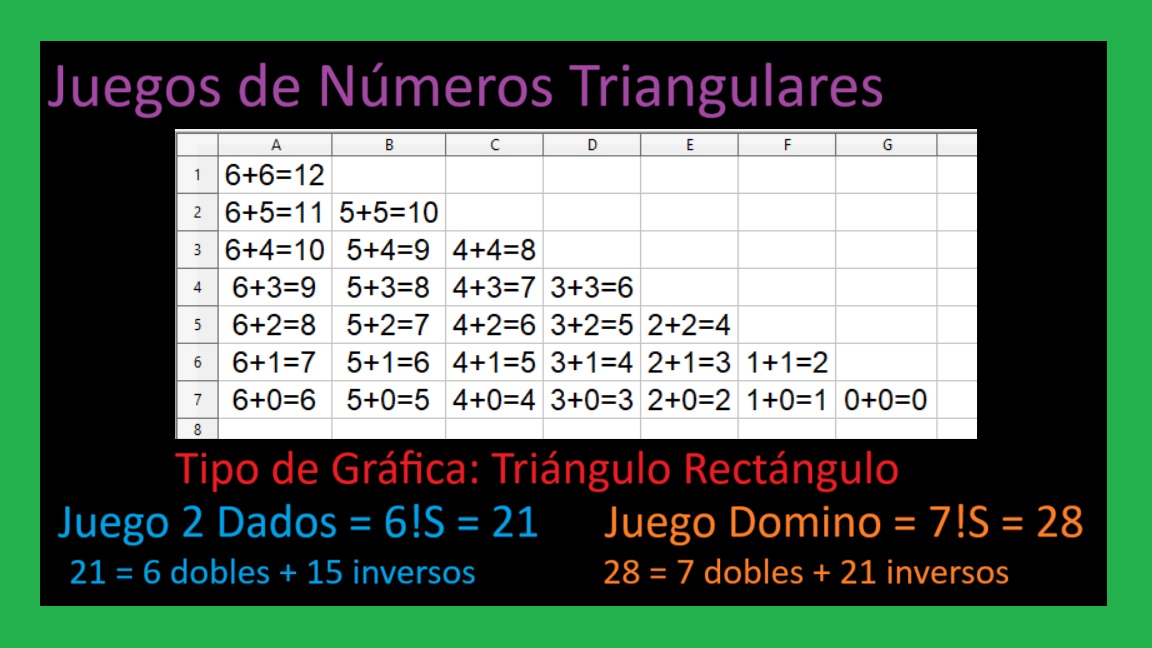
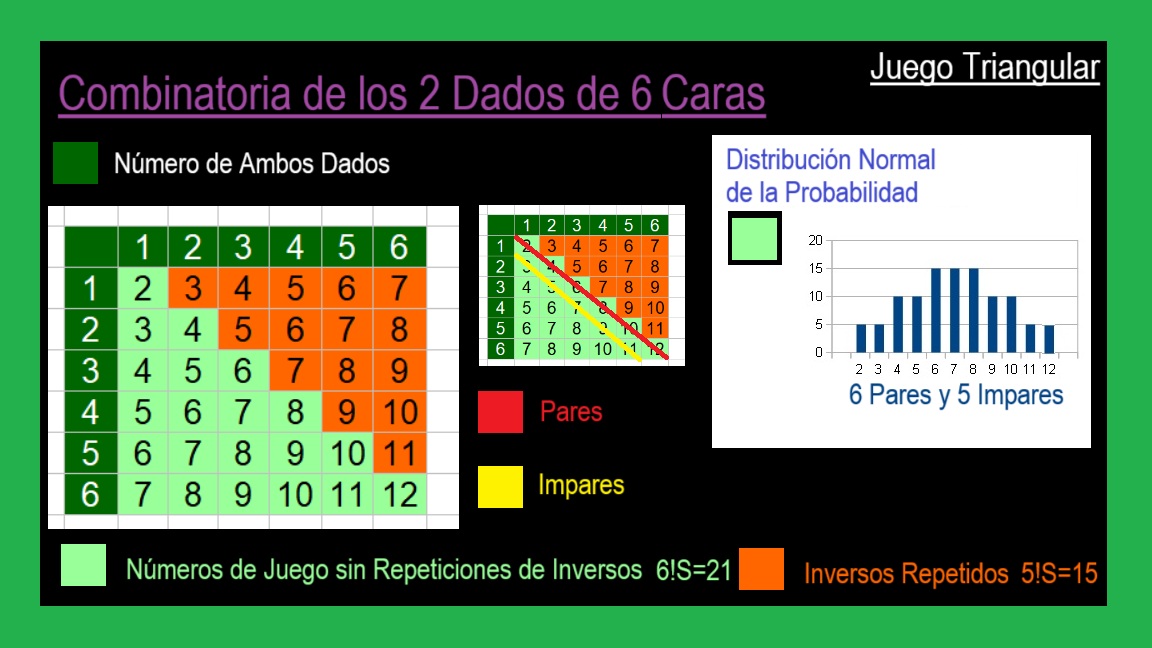
Probabilidades de los Juegos de Azar
01 Gana con las Sumas Pares en los Juegos con 2 Dados de 6 Caras

2025/10/15 11:16:17 , Miércoles
Conjeturas
Conjetura de Andrew Beal



2025/10/17 17:58:18 , Viernes
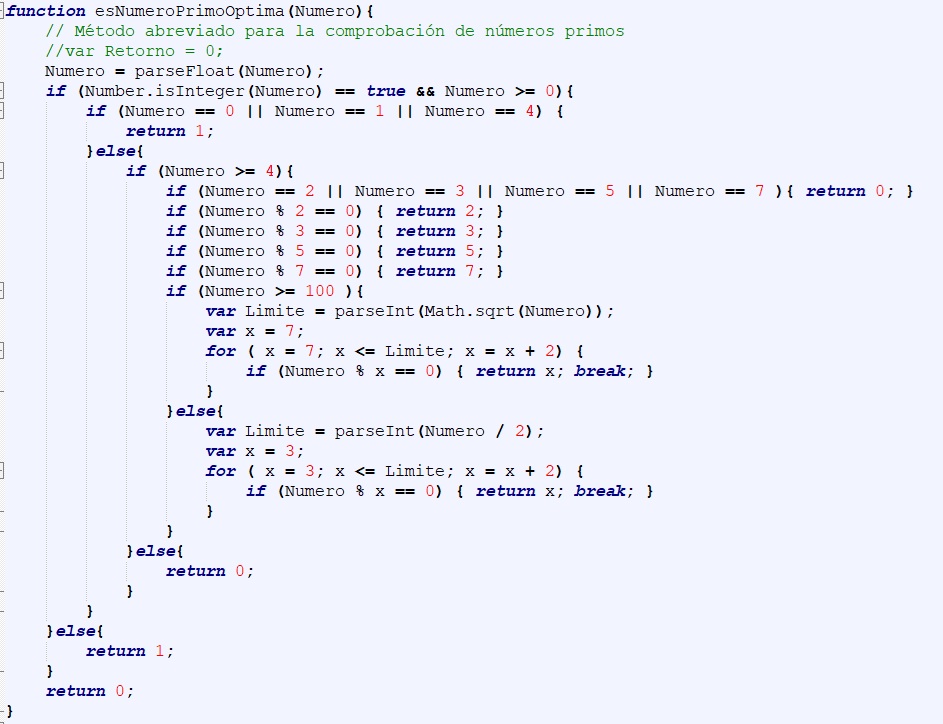
Funcion de Comprobacion de Numeros Primos
01 Esta es la Funcion en JavaScript Para Comprobar Numeros Primos
2024/07/20 14:54:53 , Sábado
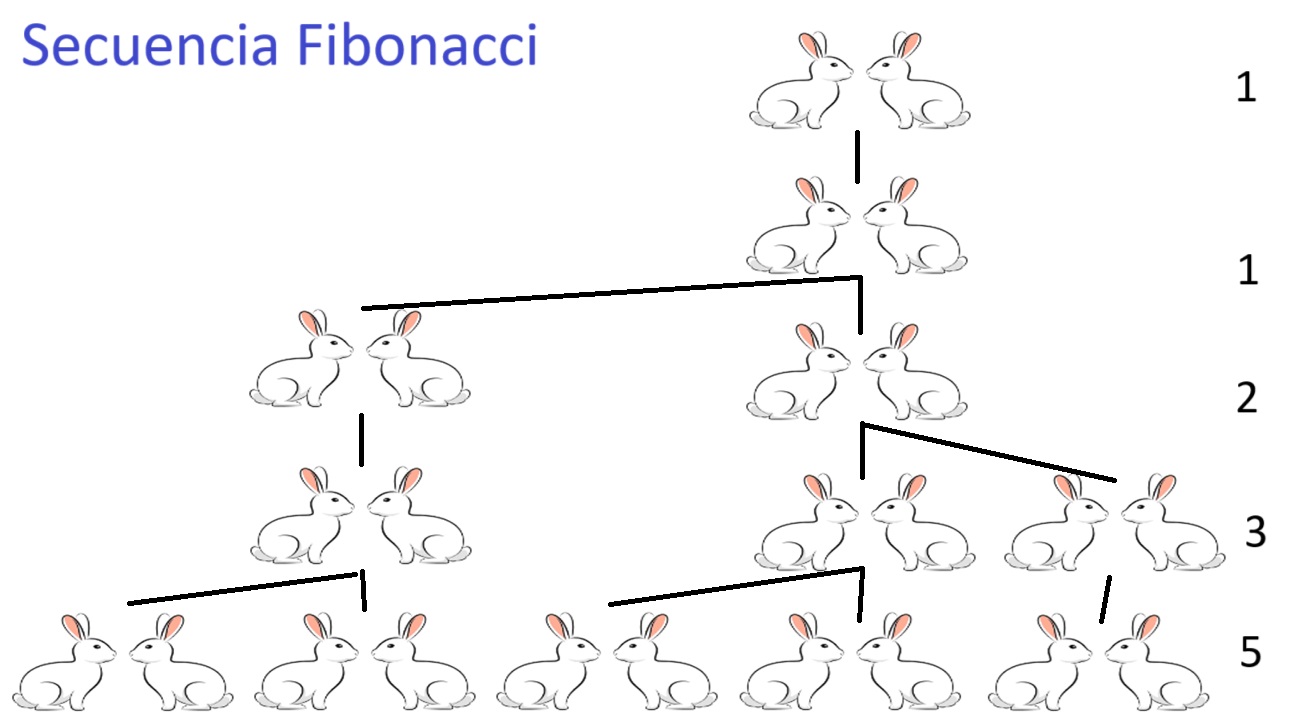
La Secuencia de Fibonacci
01 Que es la Sucesion de Fibonacci
2025/10/15 12:52:54 , Miércoles
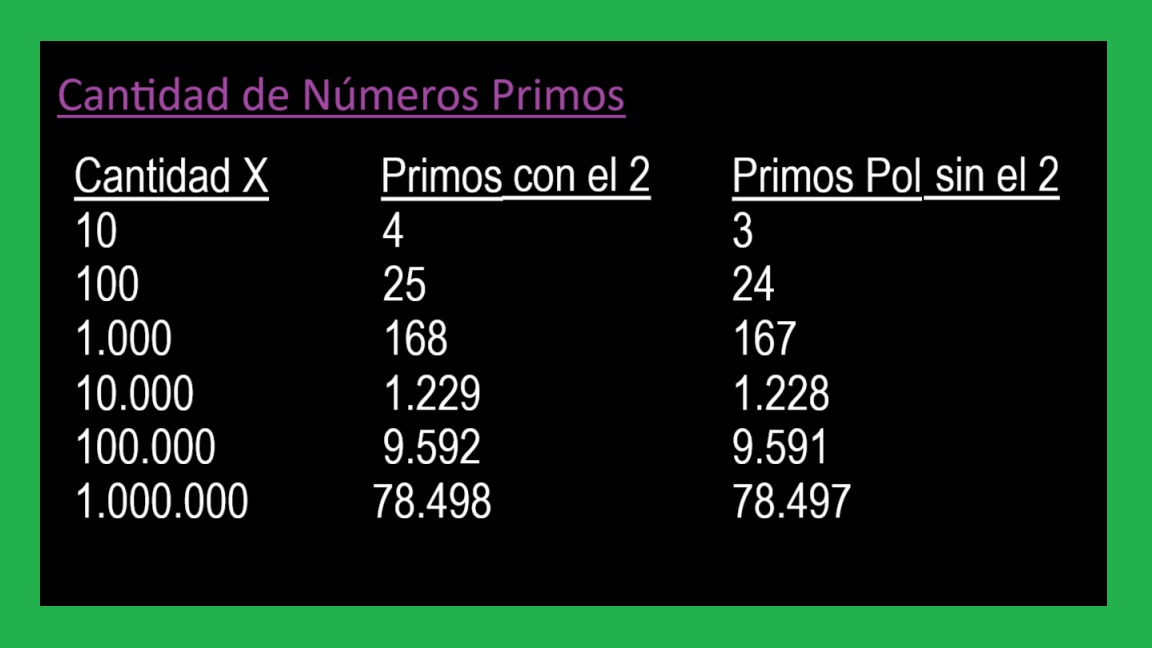
Cantidad de Numeros Primos
Cantidad de Numeros Primos con los Ante cuadrados y Factoriales de Suma
2025/04/27 11:33:05 , Domingo
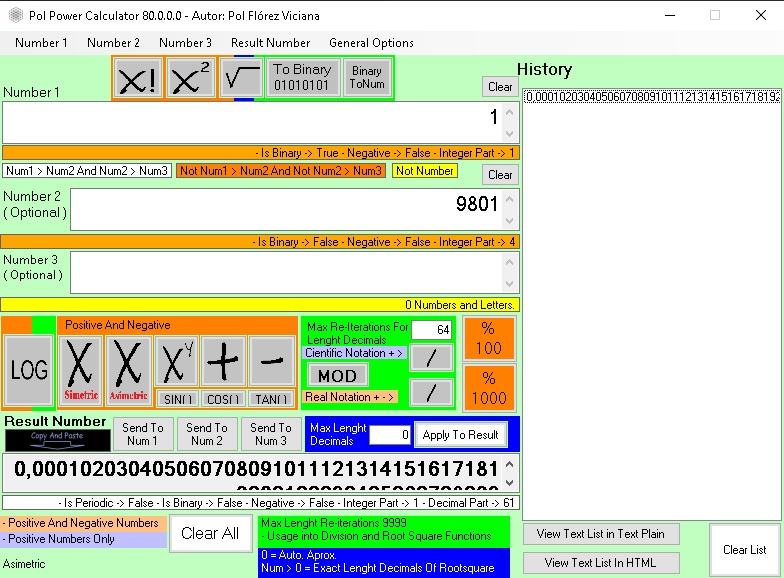
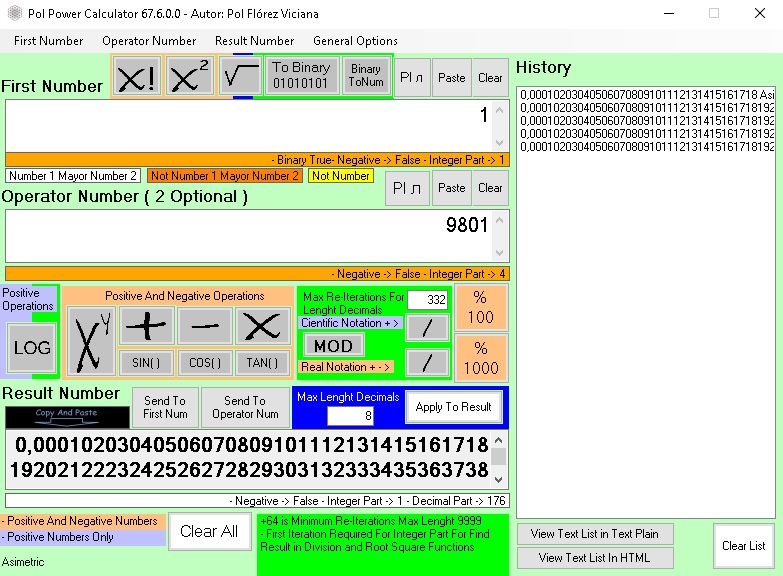
Curiosidades Matematicas de Algunos Numeros
Aproximaciones a PI con Ejemplos

2024/08/08 15:44:42 , Jueves
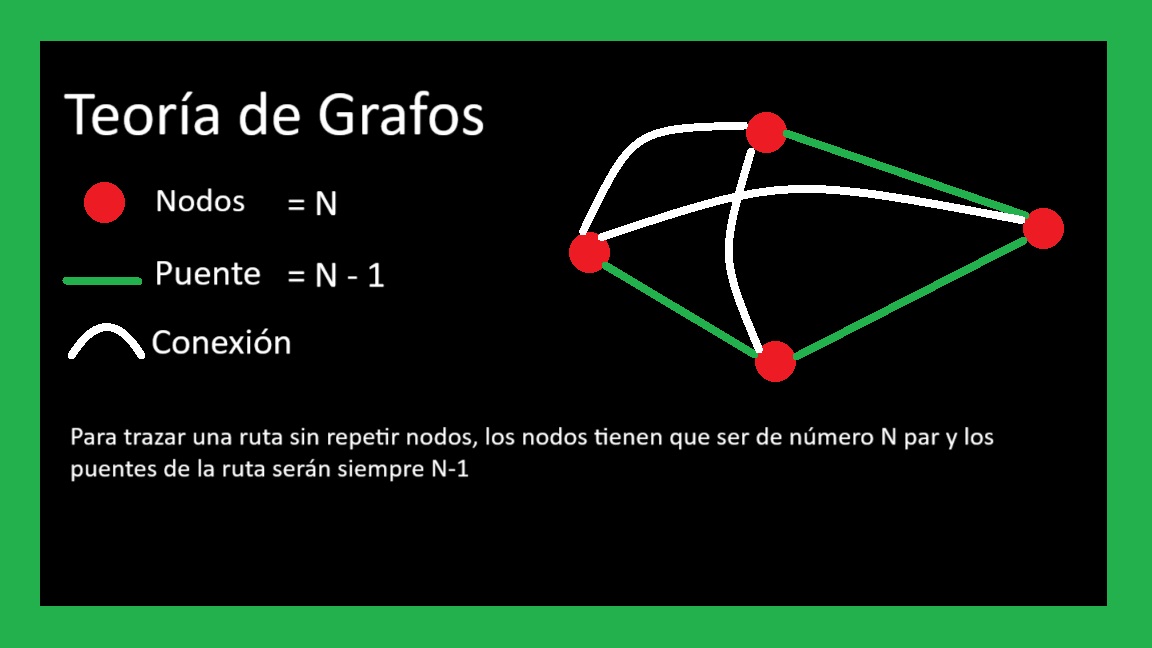
Teoria de Grafos
Teoria de Grafos en Simetrias Par
Matemáticas 2: Multiplicaciones, Divisiones, Potencias y Logaritmos
Estos Son los 24 Artículos de las Matemáticas 2: Multiplicaciones, Divisiones, Potenciaciones y Logaritmos
2025/10/12 13:48:08 , Domingo
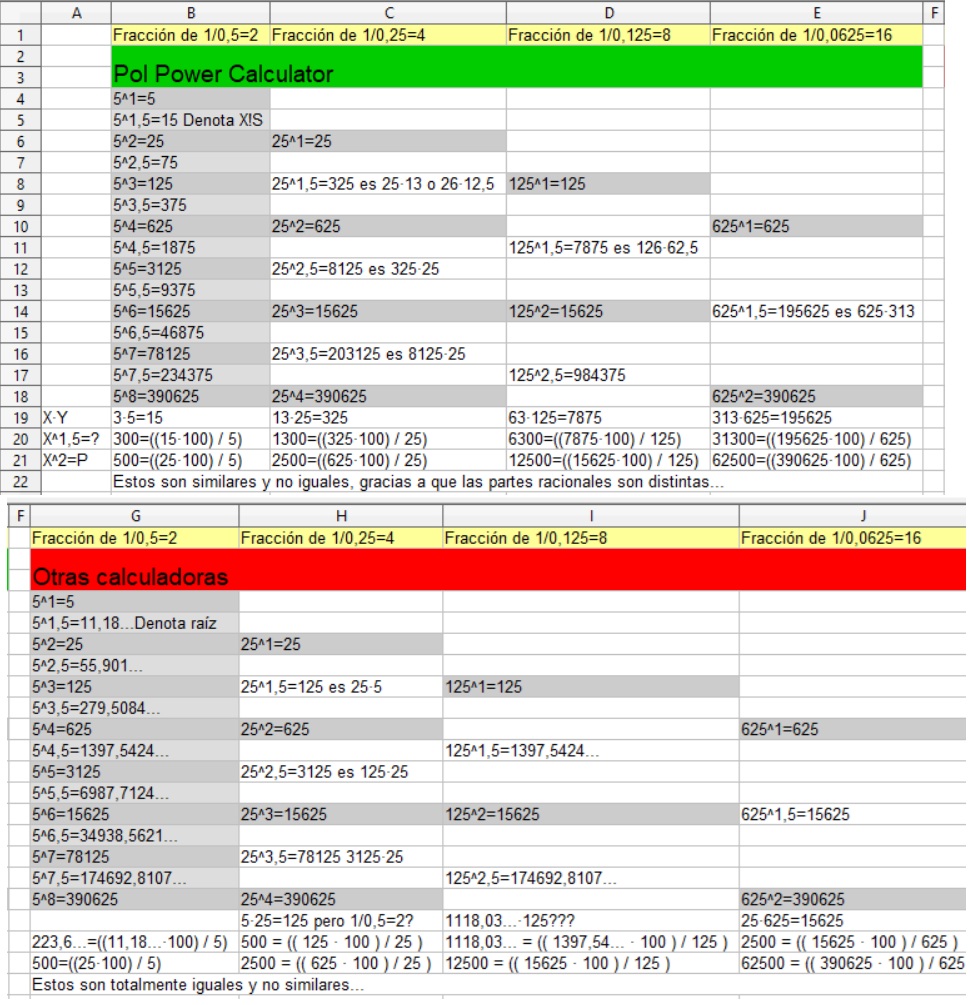
01 ¿Que es la Potenciacion?
Definicion de Potenciacion Segun Pol

2025/02/10 14:29:36 , Lunes
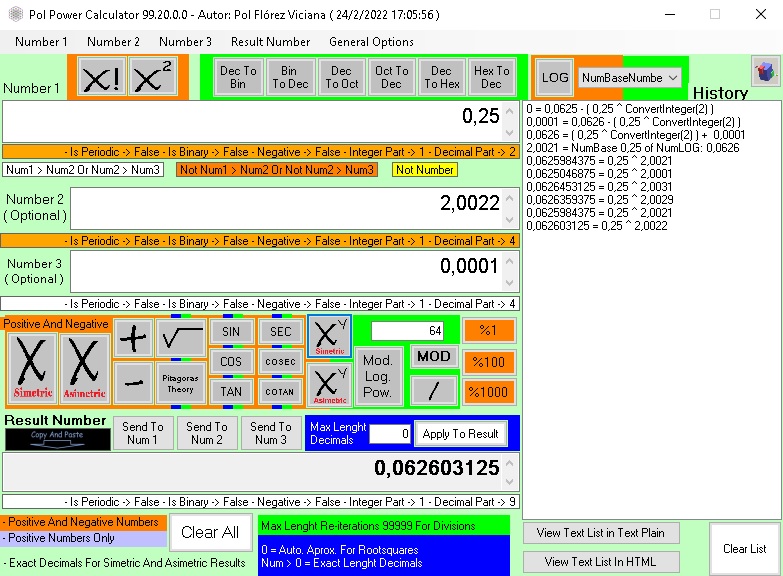
02 ¿Que es la Potenciacion Asimetrica?
Definicion de Potenciacion Asimetrica

2025/04/17 14:26:08 , Jueves
03 Tablas Varias
01 Potenciaciones de Base 10 Reales y en Notacion Cientifica


2025/04/13 19:41:50 , Domingo
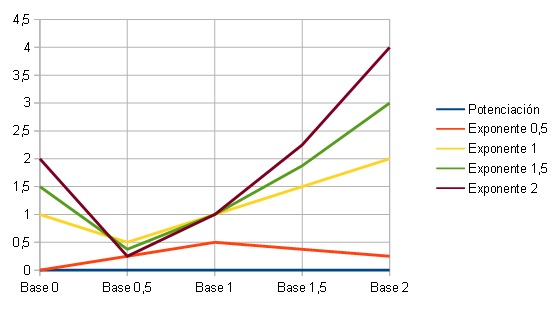
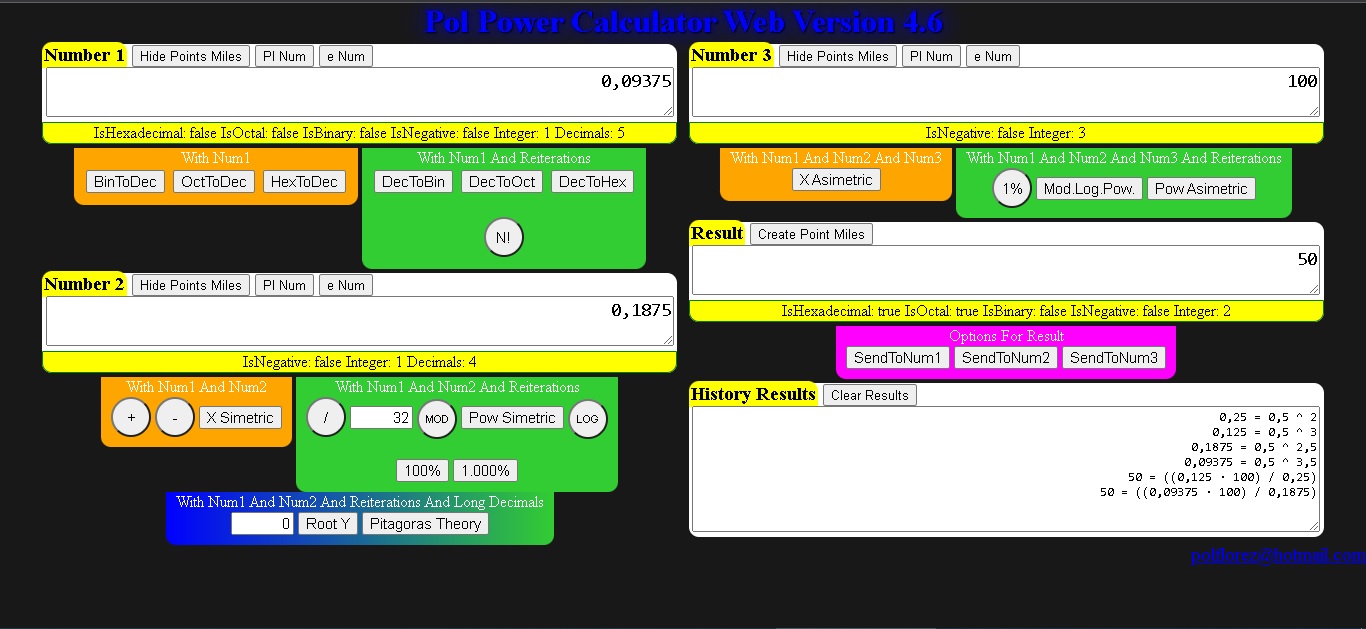
04 Las Excepciones de Potencias Entre 0 y 1
Excepciones entre 0 y 1 en Potencias de las Pol Power Calculator
2025/10/02 15:09:33 , Jueves
05 Propiedades Compartidas de Potencias de Exponente Entero y Racional
01 Relaciones Entre Factoriales de Sumas y Cuadrados


2025/01/20 15:45:42 , Lunes
06 ¿Que es la Tetracion?
01 Definicion de Tetracion Segun Pol

2025/10/02 12:57:03 , Jueves
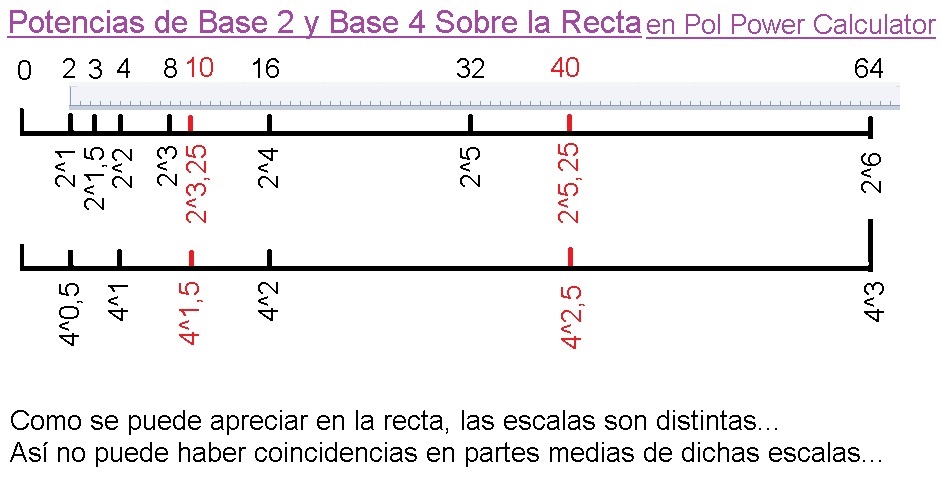
07 Ley de Proporcionalidad de Potencias en las Pol Power Calculator
Proporciones Adecuadas de las Potencias Situadas Sobre la Recta


2025/01/06 15:21:40 , Lunes
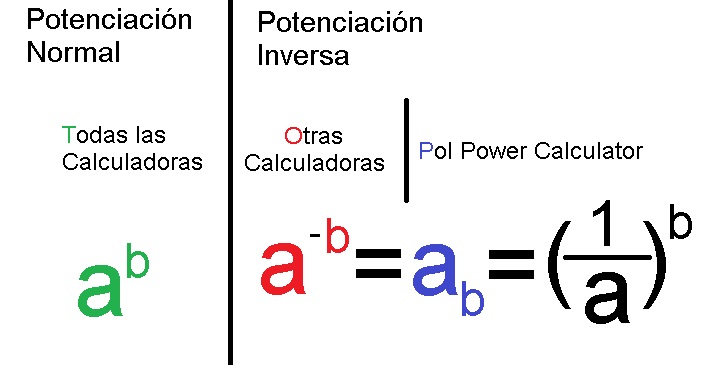
08 ¿Como Diferenciar Sin Signos una Potencia Normal de una Potencia Inversa?
Diferenciar la Potencia Normal de la Potencia Inversa

2025/09/23 16:37:49 , Martes
09 Propiedades de Potencias
01 Propiedades de las Potencias

2025/10/18 11:10:33 , Sábado
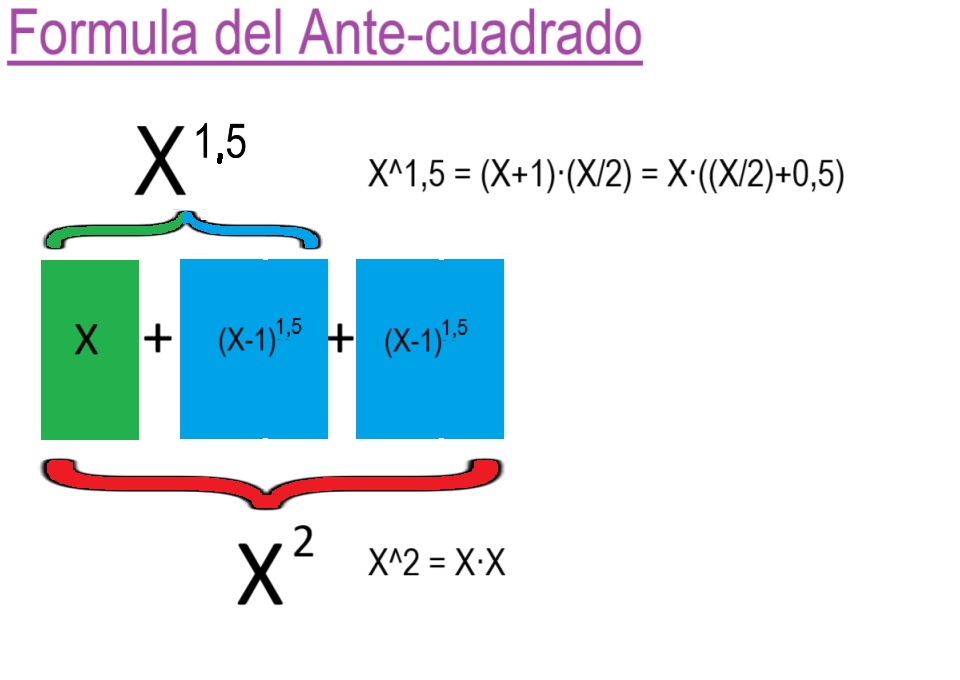
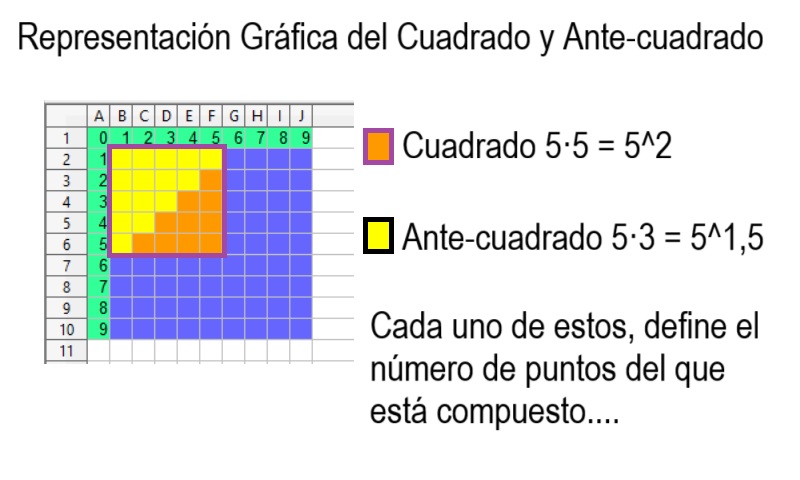
10 Tipos de Potencias Antecuadradas y Anticuadradas
01 1 Definicion de Numero Antecuadrado

2025/09/20 17:58:34 , Sábado
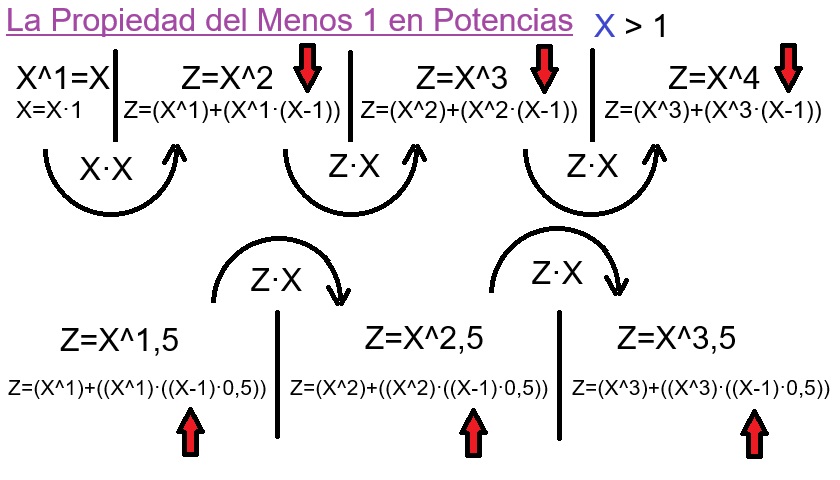
11 Diferencia Proporcional de Potencias de Exponente Entero y Racional
La Base 2 es la Unica Que es Simetrica Naturalmente


2025/10/02 12:19:56 , Jueves
La Simetria Natural Perfecta de la Base 2
La Simetria Natural Perfecta en la Base 2

2025/10/02 16:01:45 , Jueves
01 ¿Que es el Logaritmo?
01 Definicion de Logaritmo Segun Pol

2025/05/20 15:46:26 , Martes
La Funcion Logaritmo en las Pol Power Calculator
La Funcion Logaritmo es Parecida a la Funcion Dividir

2025/07/15 12:12:48 , Martes
Propiedades de los Logaritmos
Propiedades de los Logaritmos

2025/10/11 16:55:40 , Sábado
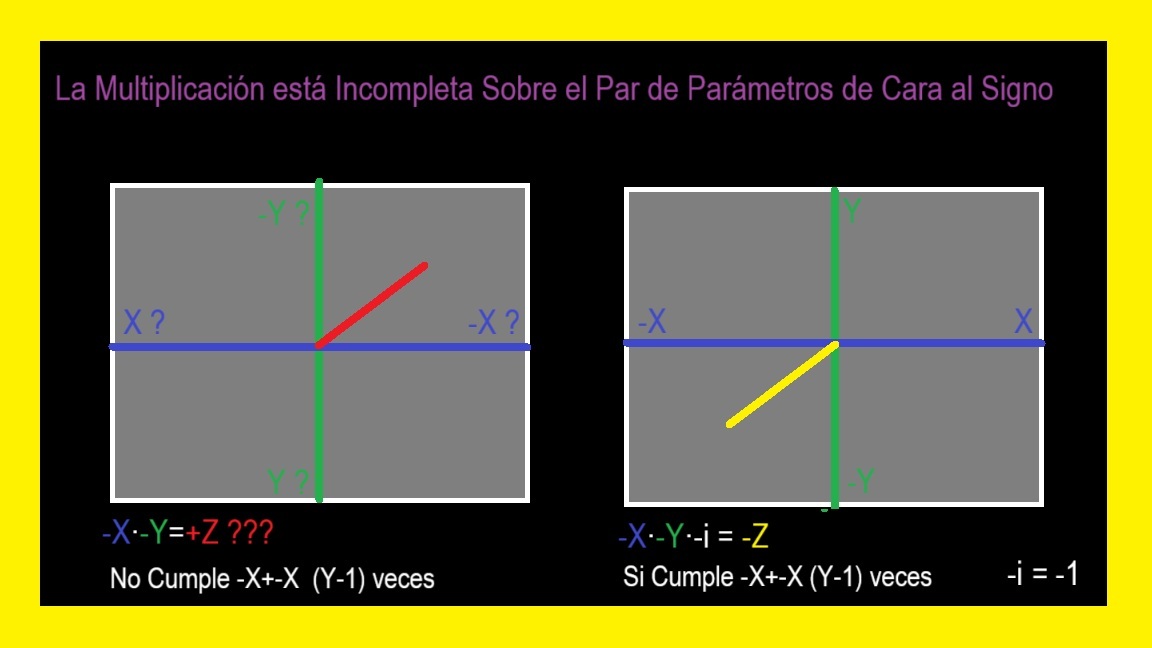
01 ¿Que es la Multiplicacion?
01 Definicion de Multiplicacion Segun Pol

2025/01/28 13:06:48 , Martes
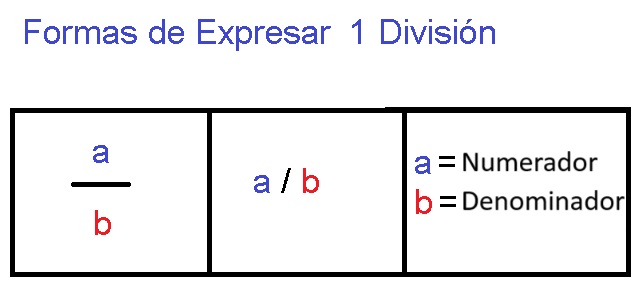
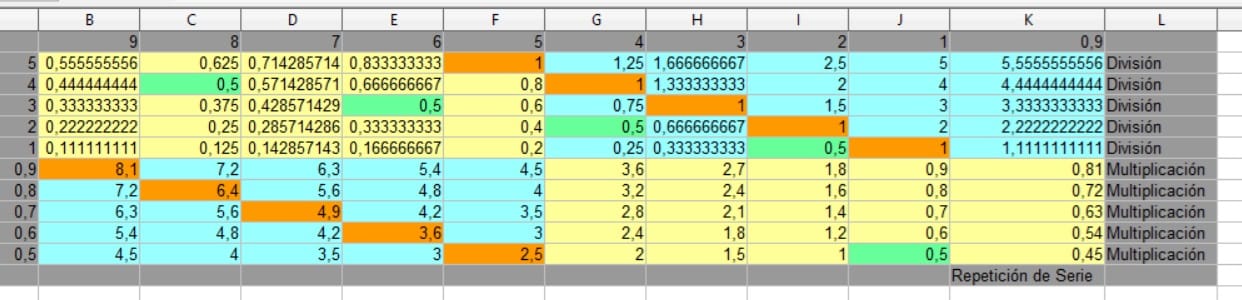
02 ¿Que es la Division?
Definicion de Division Segun Pol
2023/05/06 13:16:39 , Sábado
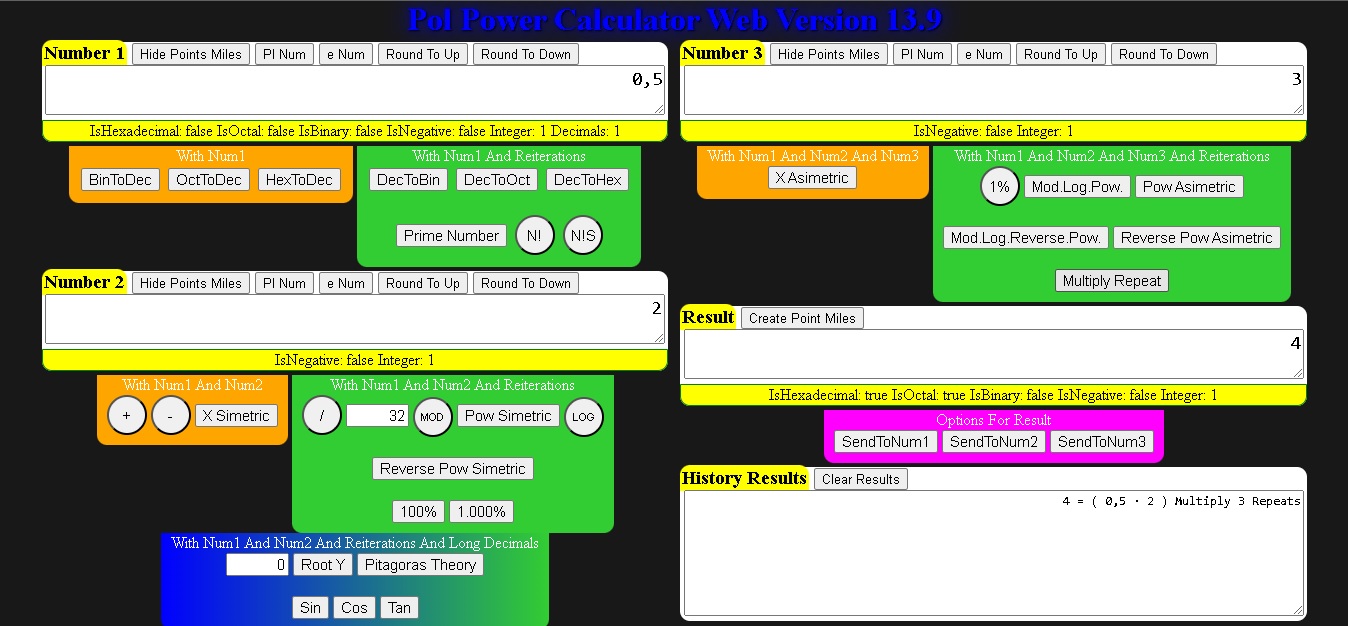
El Boton Especial de Potencia Multiply Repeat
El Boton de Funcion Multiply Repeat
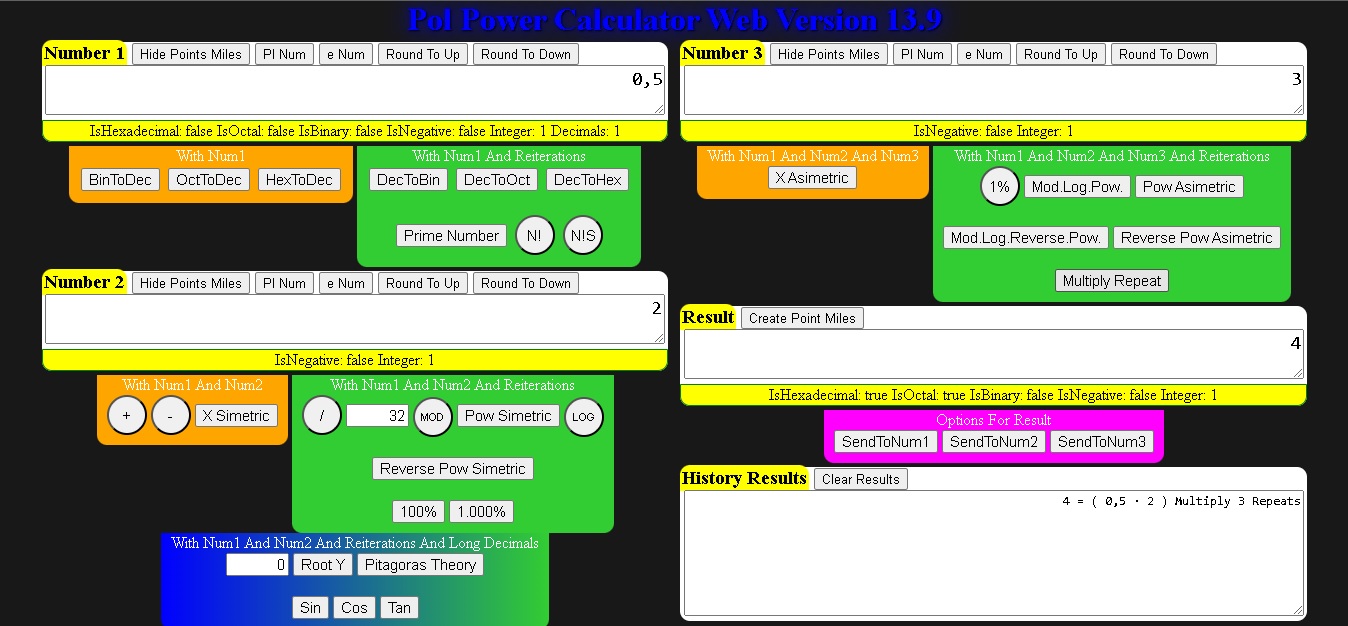
2025/10/11 18:31:34 , Sábado
Normas de las Multiplicaciones
Normas al Multiplicar Numeros



2025/08/11 21:12:00 , Lunes
¿Que es el Porcentaje?
01 Definicion de Porcentaje Segun Pol

2025/01/06 15:58:23 , Lunes
¿Que es la Multiplicacion Asimetrica?
Definicion de Multiplicacion Asimetrica
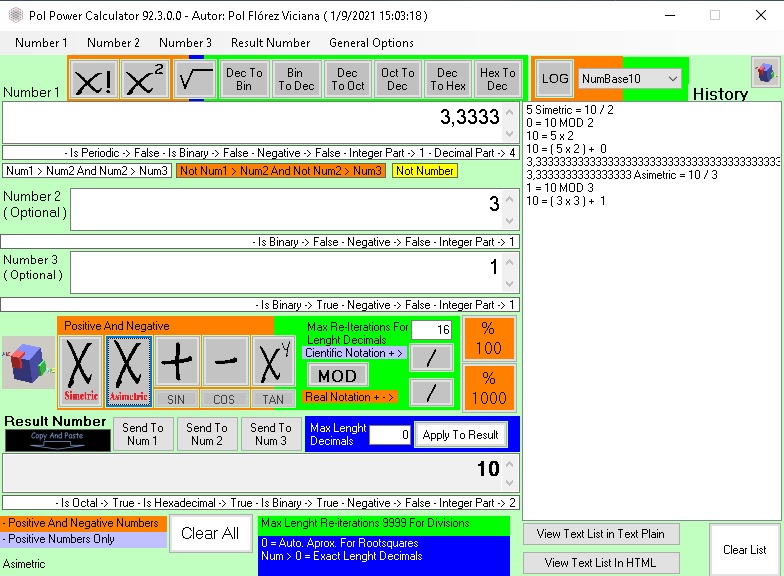

2025/09/23 15:17:43 , Martes
Ley de Signos o de Polaridad Numerica Entre Operadores
01 La Necesaria Ley de Signos en Potencias
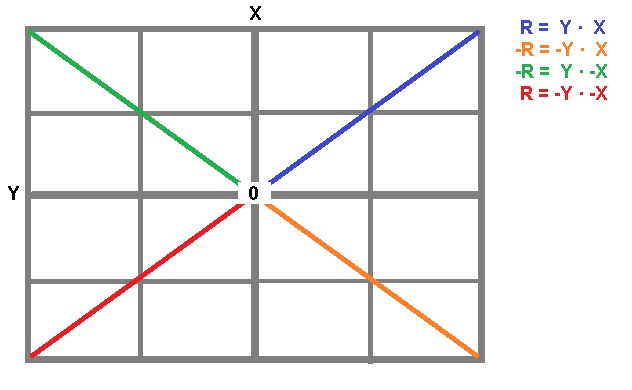
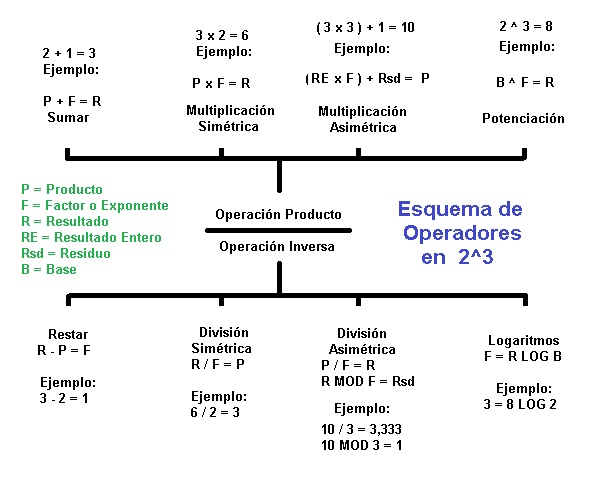
2024/05/16 20:17:42 , Jueves
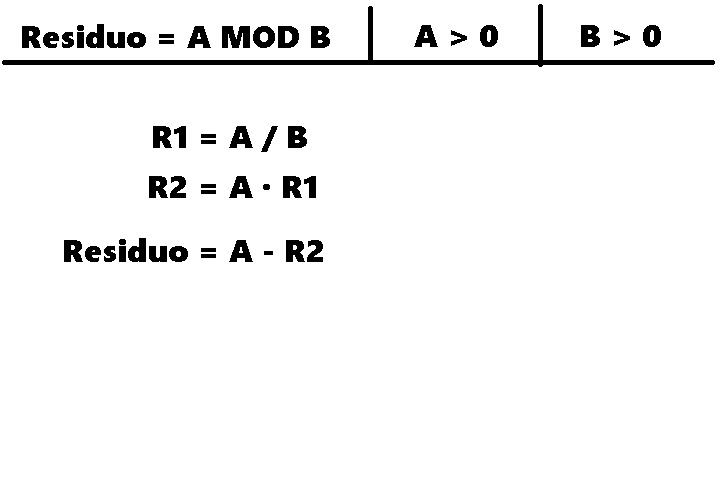
¿Que es el Residuo en las Divisiones MOD?
El Boton MOD de Residuo en las Divisiones
2024/12/03 17:37:26 , Martes
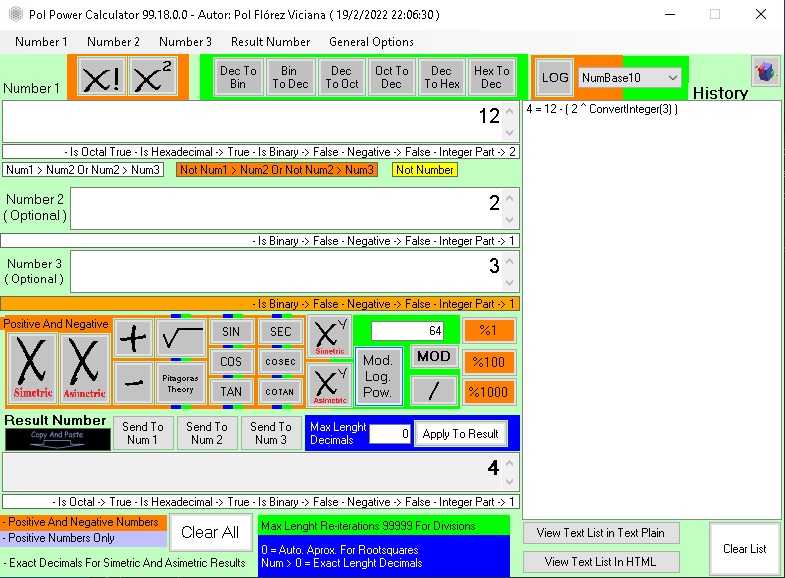
¿Que es el Residuo en los Logaritmos MOD.LOG.POW?
El Boton MOD.LOG.POW de Residuo del Logaritmo
Matemáticas 3: Factoriales, Raíces, Cambios de Base y Trigonometría
Estos Son Los 19 Artículos de Matemáticas 3: Factoriales, Raíces, Cambios de Base y Trigonometría
2025/10/12 18:39:19 , Domingo
01 ¿Que es el Factorial?
01 Definicion de Numero Factorial Segun Pol


2025/10/13 17:49:17 , Lunes
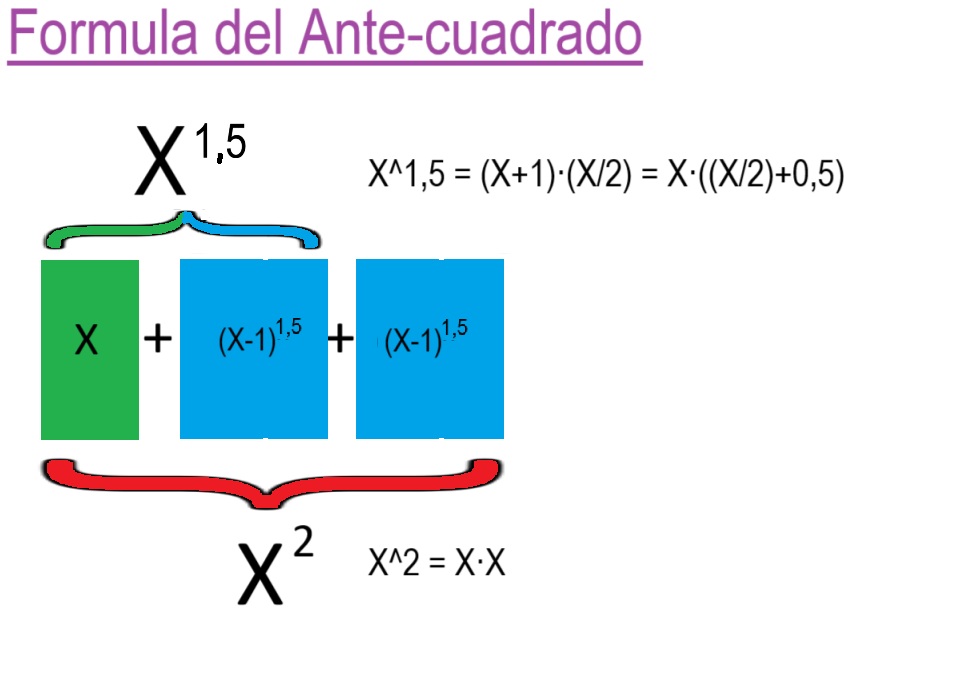
02 ¿Que es el Factorial de Sumas?
01 Definicion de Factorial de Suma Segun Pol


2025/05/31 14:24:53 , Sábado
03 Los Factoriales y las Series
01 Los Factoriales Tambien son Series de Numeros



2025/03/30 18:48:20 , Domingo
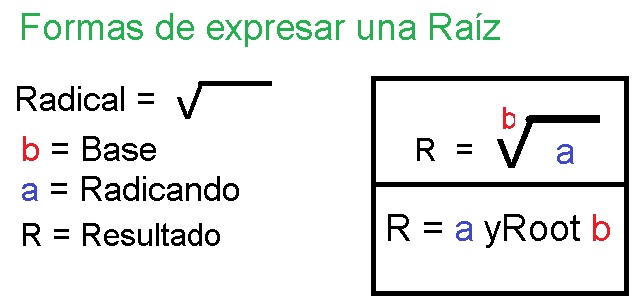
01 ¿Que es una Raiz?
Definicion de Raiz o Radical Segun Pol


2025/01/06 14:49:31 , Lunes
02 ¿Como Hacer Raices o Radicales?
1 Proceso Para Hacer Una Raiz de Cualquier Base Mayor a 1



2023/09/21 17:48:38 , Jueves
03 La Limitacion de las Raices en las Pol Power Calculator Hasta la Base 128
El Limite de Base 128 Para Raices

2025/01/06 15:42:20 , Lunes
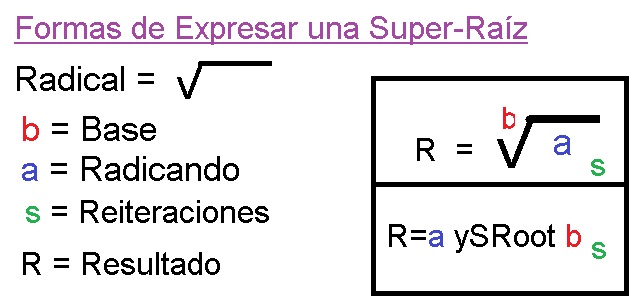
04 ¿Que es una Super Raiz?
Definicion de Super Raiz Segun Pol
2025/08/16 22:35:02 , Sábado
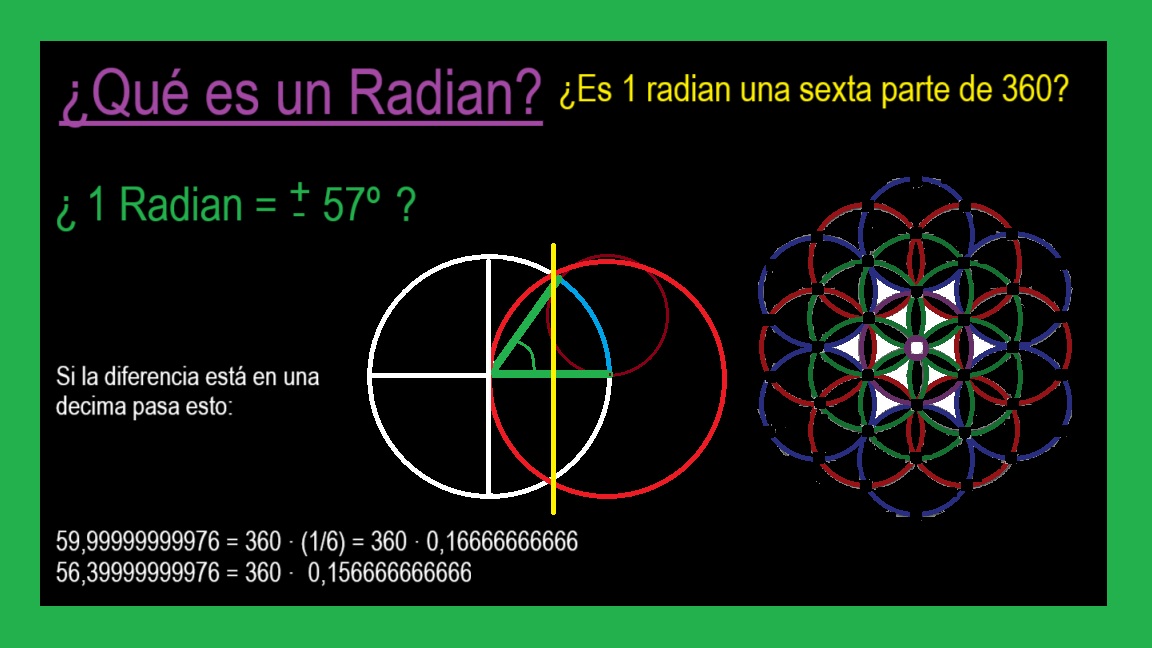
01 ¿Que es la Trigonometria?
01 Definicion de Trigonometria Segun Pol


2024/09/16 16:40:09 , Lunes
Seno, Coseno y Tangente
La Importancia de los Lados de un Triangulo Rectangulo


2025/05/31 12:17:40 , Sábado
01 ¿Que es la Geometria?
01 Definicion de Geometria Segun Pol



2025/01/06 16:03:18 , Lunes
02 ¿Que son los Poligonos?
Definicion de Poligono Segun Pol

2024/03/23 19:18:01 , Sábado
03 ¿Que son los Poliedros?
1 Los Poliedros Regulares, son los Solidos Platonicos

2025/10/13 16:08:44 , Lunes
04 Teorema de Pitagoras
01 01 Definicion del Teorema de Pitagoras



2025/07/09 13:41:37 , Miércoles
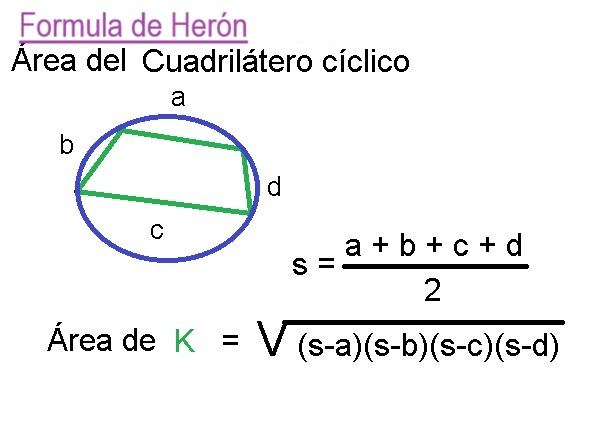
05 Calculo de Areas, Volumenes, y Perimetros
01 01 Ecuaciones Para Calcular Areas de Superficies


2024/03/23 19:18:17 , Sábado
El Problema del Cuadrito del Infinito
01 El Problema del Cuadrito de Mas

2024/12/15 16:16:29 , Domingo
¿Como Cambiar Entre Bases en JavaScript?
01 Cambios de Base

2025/05/02 16:19:38 , Viernes
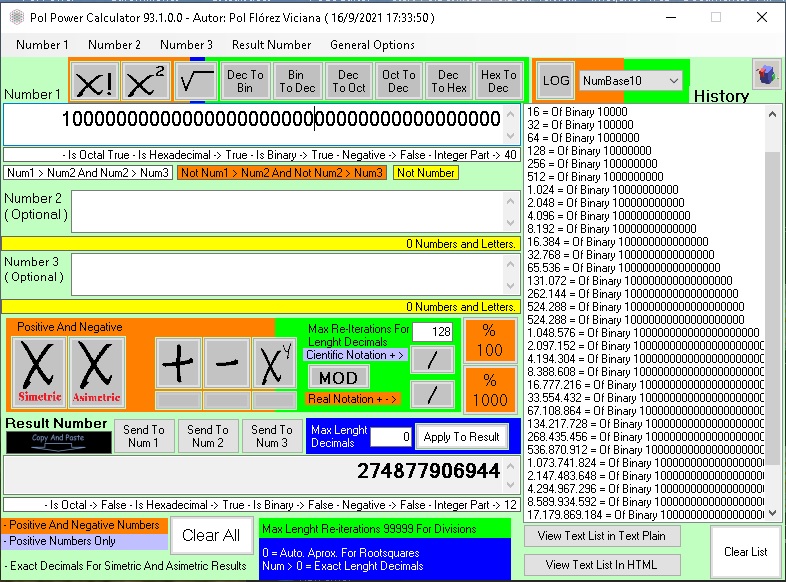
¿Como Convertir de Decimal a Binarios y de Binario a Decimales?
Convierte de Binario a Decimal y a la Inversa

2025/05/02 16:33:52 , Viernes
¿Como Convertir de Decimal a Hexadecimales y de Hexadecimal a Decimales?
Convierte de Hexadecimal a Decimal y a la Inversa

2025/05/02 16:39:36 , Viernes
¿Como Convertir de Decimal a Octales y de Octal a Decimales?
Convierte de Octal a Decimal y a la Inversa
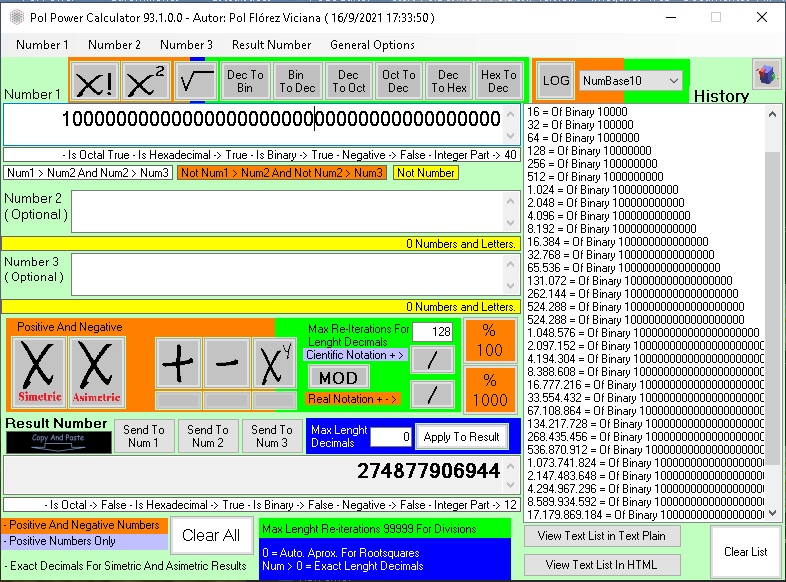
Matemáticas 4: Matemáticas con las Calculadoras Pol Power Calculator
Estos Son Los 16 Artículos de Matemáticas 4: Matemáticas con las Calculadoras Pol Power Calculator
2024/01/01 14:54:25 , Lunes
Significado de las Zonas de Colores en las Pol Power Calculator
01 Naranja; No Tienen Limites
2025/10/14 12:41:53 , Martes
Errores en Potencias de Otras Calculadoras
01 Razon de la Falta de Decimales



2025/10/17 16:04:03 , Viernes
La Historia de los Inversos en Potencias
Los Inversos No son lo Que Parecen
2025/09/03 15:01:57 , Miércoles
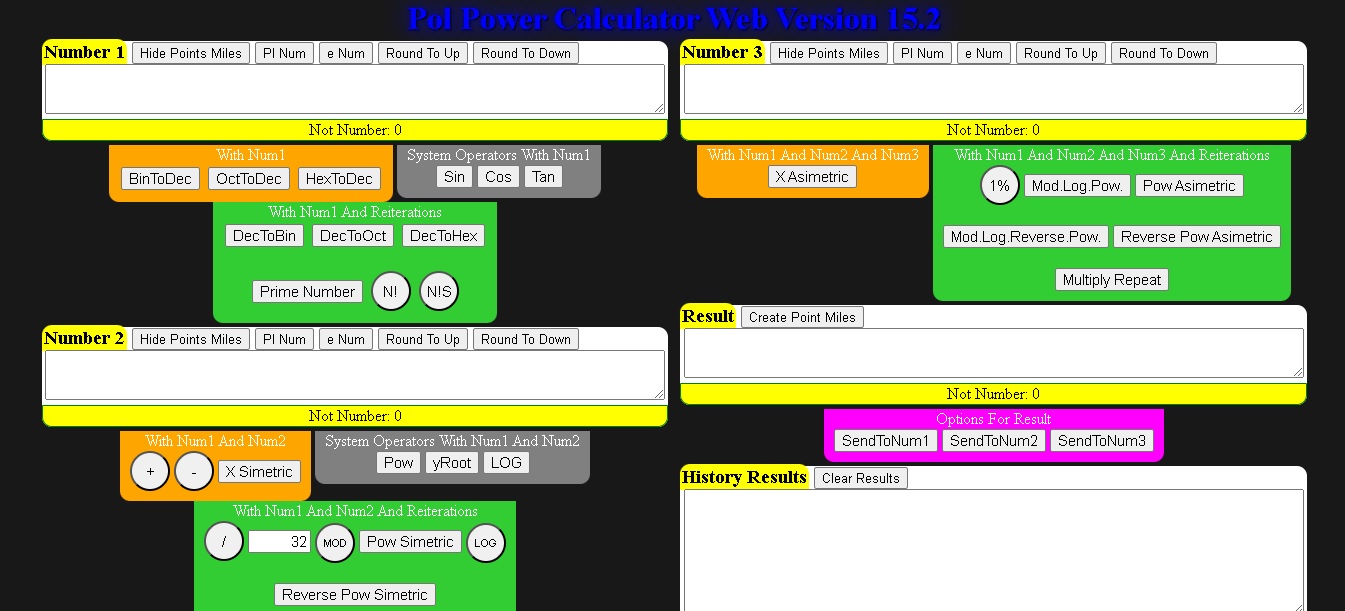
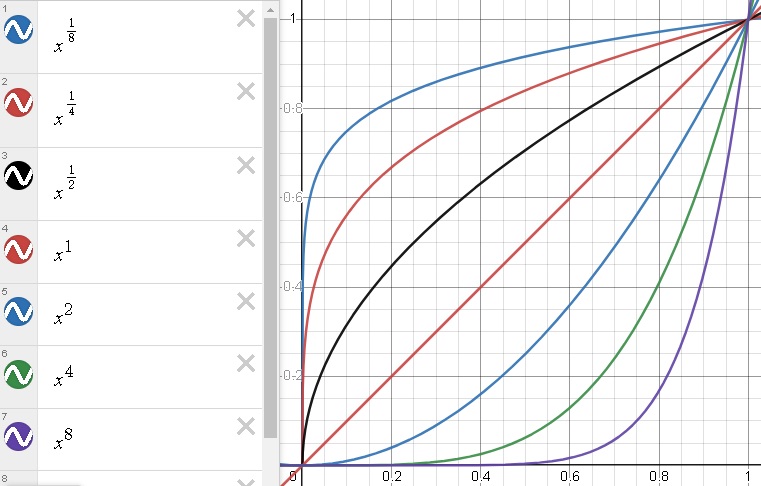
La Logica de Potencias de Exponente Entero y Racional
Lo Logico de lo Evidente; Los Racionales de los Exponentes
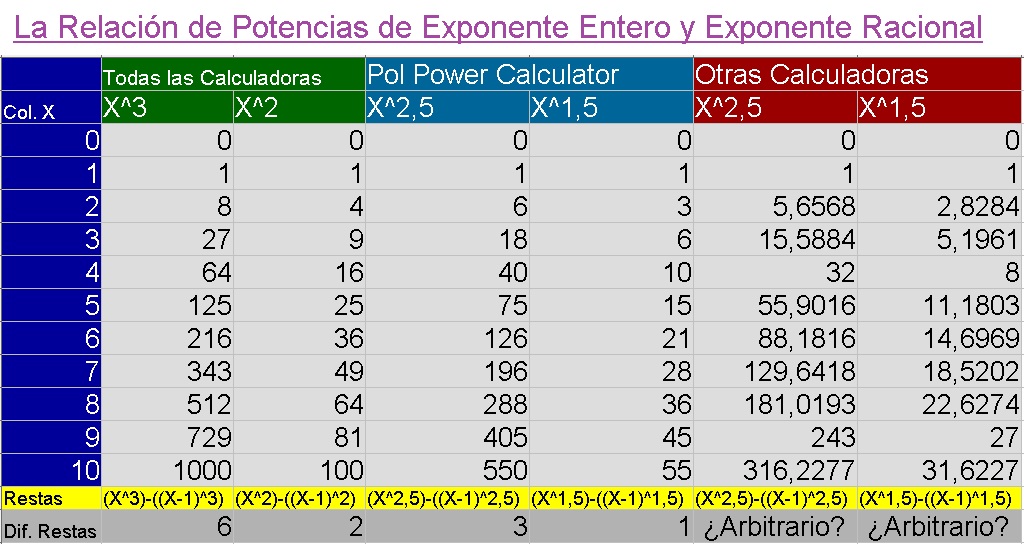

2025/05/12 12:36:00 , Lunes
La Proporcion de Multiplicaciones en Potencias
La Proporcion Implica Que No Sean Equitativos Por Esto


2025/09/03 15:02:14 , Miércoles
Los Errores de Otras Calculadoras No Son Errores
Los Errores No Son Errores Siendo Estos Pasos Adelantados

2025/02/18 13:56:46 , Martes
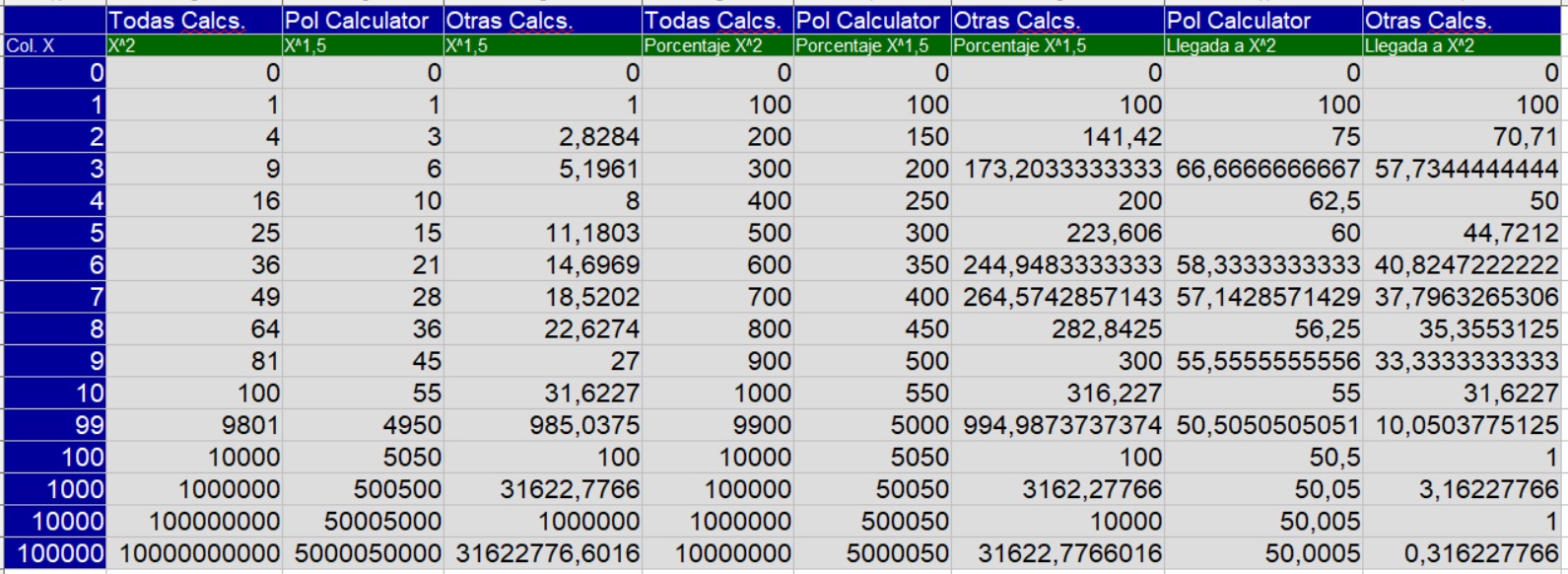
Los Saltos en Potencias de Otras Calculadoras
01 El Salto en Exponentes Racionales de Potencias en las Pol Power Calculator


2025/03/31 14:33:17 , Lunes
Suma o Multiplicacion de Potencias
01 Sumar o Multiplicar es la Cuestion

2025/04/12 16:24:41 , Sábado
Teorias Sobre Potenciaciones
Pol Power Calculator vs Otras Calculadoras

2023/09/30 17:44:22 , Sábado
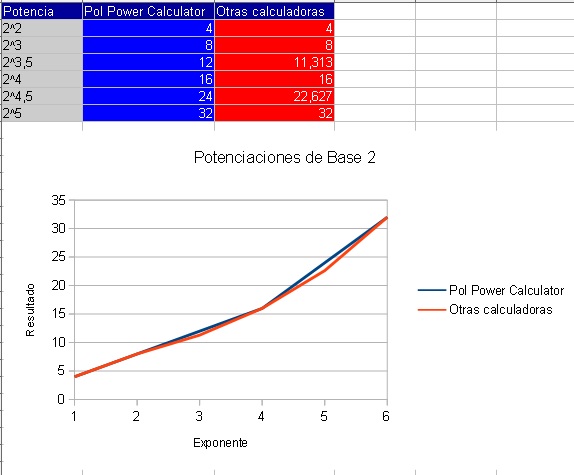
¿Donde No Hay Errores en Todas las Calculadoras?
Donde No Hay Errores en Todas las Calculadoras
2025/09/03 15:03:24 , Miércoles
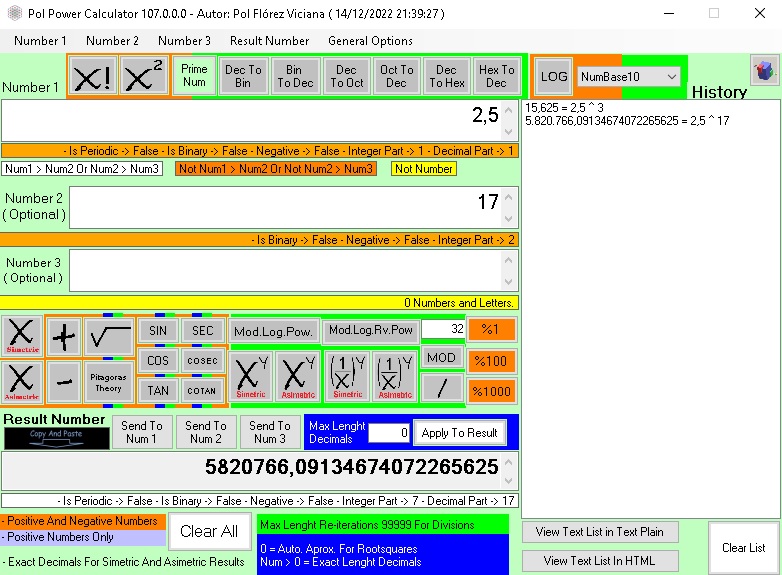
01 ¿Que Pasa Con Solo 20 Digitos y 16 Decimales?
01 El Principal Problema de Algunas Calculadoras
2024/01/11 14:53:46 , Jueves
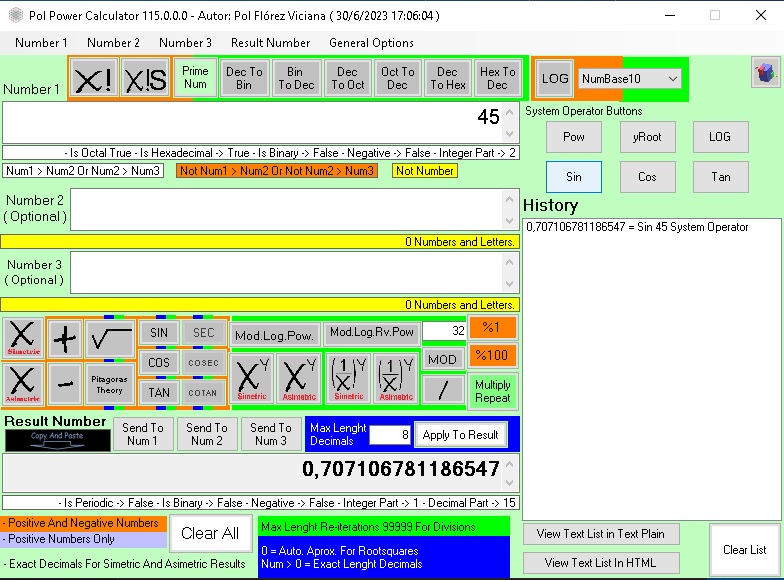
02 Calculadora Sin Limite de Digitos
01 Las Calculadoras Pol Power Calculator Sin Limite de Digitos

2023/12/15 14:40:14 , Viernes
Resolver 1 Logaritmo de Numeros Reales
1 Hacer Un Logaritmo de Numero Real de Base Mayor a 1


2023/09/30 22:06:09 , Sábado
Resolver 1 Potencia con Exponente Racional
Como Hacer 1 Potencia de Exponente Racional Segun Pol

2025/09/03 15:04:04 , Miércoles
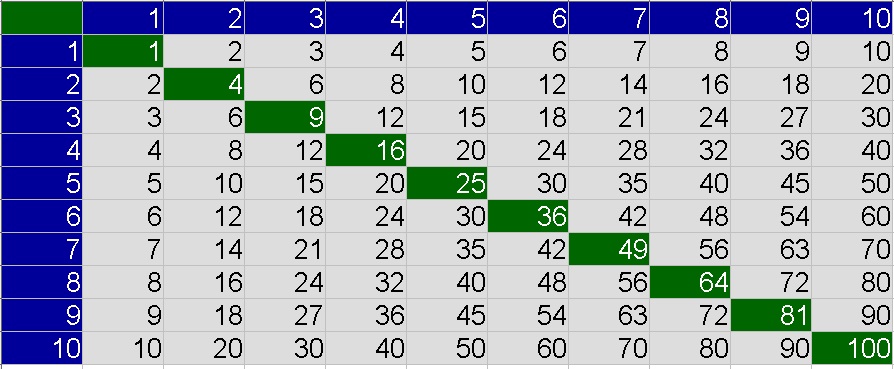
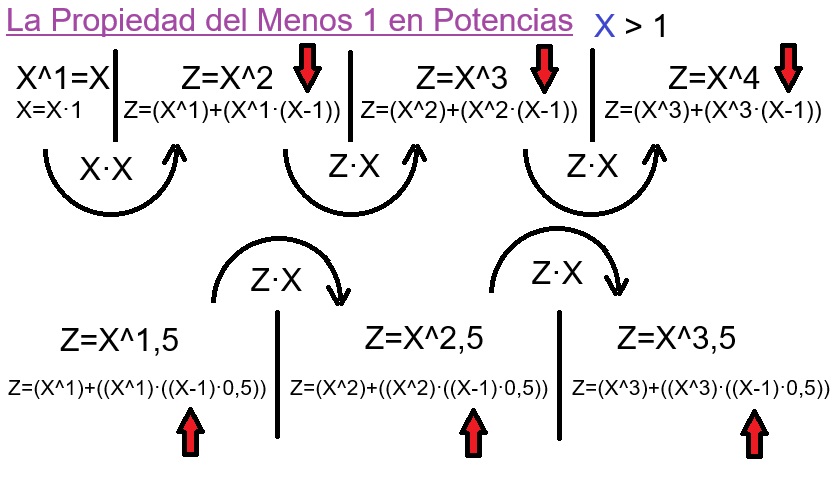
Las Potencias Normales e Inversas
Los Resultados de Potencias Normales e Inversas

2023/09/24 16:32:06 , Domingo
Problemas Resueltos con las Pol Power Calculator
01 Problemas de Raiz Cubica de Suma de Potencias